21. Mutationem motus proportionalem esse vi motrici impressae

I

Two recently published books offer their services as an aid for the reader who wants to understand Sir Isaac Newton's Principia of 1687: N. Guicciardini's Reading the Principia[1], and I.B. Cohen's A Guide to Newton's Principia, an introduction to a new translation of Newton's magnum opus by I.B. Cohen and Anne Whitman from Newton's Latin into English[2]. But Guicciardini and Cohen confusingly differ substantially in their presentations of Newton's most elementary principle, the concept of force, which Newton introduces with his second law of motion, and, unfortunately, both of them fail to meet its true sense.

The second law of Newton's theory of force and motion mathematically connects the concept of force as cause with its effect on the motion of a body[3]. In Newton's Latin, the law in its main contents reads Mutationem motus proportionalem esse vi motrici impressae[4]. Cohen and Whitman render these words correctly into A change in motion is proportional to the motive force impressed. I.B. Cohen in his Guide points out that Newton here introduces a concept of impulsive force because this force produces finite velocities, respectively finite motions, respectively finite changes in the motion of a body[5]. Since Newton defines motion by the product mass times velocity (Principia, def. 2), in using the symbols m for mass and v for velocity we shall be allowed to symbolize Newton's term change in motion by Δ(mv) — vector notation omitted[6]. Newton's impressed motive force, if symbolized by F_i, should then fulfill the proportion F_i ∝ Δ(mv) or, if rendered into an equation, F_i = Δ(mv) × C, with C serving as constant of proportionality.

Obviously such an impulsive force vis motrix impressa F_i differs from the common view of Newton's second law to introduce the concept of a continuous force, F_c = m(dv/dt) = d(mv)/dt = ma (with a = acceleration), which concept classical mechanics is based on. Most significantly, this classical textbook concept lacks the constant of proportionality C to mathematically connect the cause force with its proportional effect on motion.

Guicciardini, though he explicitly takes the Cohen-Whitman translation as a basis, without making any reference to Cohen's different presentation simply presupposes and maintains the „classical" view of the second law by implicitly alleging its consistency with Newton's words[7]. Thus he eludes a conflict between Newton's and the „classical" concept of force, of which Cohen, on the other hand, is well aware. Cohen attacks the matter frontally by explicitly alleging that Newton didn't need to distinguish between the „impulsive" and the „continuous" form of „force", nor had he to bother with constants of proportionality to arise from different concepts of „force", rather he „avoided the problem of dimensionality because he was dealing with ratios rather than equations"[8], and in general: „because the Principia sets forth a dimensionless physics"[9].

Alas! The famous Principia, the bible of classical mechanics, which Newton based on the art of measuring by the help of geometry[10], „a dimensionless physics"? Is not the dimension of a physical magnitude the geometric measure of the magnitude? Is not the aim to measure physical magnitudes such as times, spaces, forces, velocities, motions, accelerations etc. the central concern and object of Newton's theory of motion? Didn't experimental philosophy in general start with Galileo's successful attempt to measure the constant acceleration of uniformly accelerated motion through the ratio of velocity and time, i.e. to identify the dimension [v/t = L/T²] of acceleration, expressed and measured in units of space [L] and time [T]? And why, for Heaven's sake, does Cohen allege and believe that a theory of motion which deals with ratios and proportions instead of equations „avoids the problem of dimensionality"? Is it not true that Galileo's and Newton's theory is a quantitative geometric theory of motion, i.e. a theory of measurement of motion in terms of times and spaces, even if presented not in equations? How could such a theory ever be mathematically consistent, had it not first solved the problem of measurement, equal measurement of equal magnitudes, different measurement of different, including the consideration of consistent constants of proportionality — all of which is the „problem of dimensionality"? Should not a „dimensionless physics", then, be a contradiction in terms?

II

A careful mathematical research with respect to the measurement or the dimensions of Newton's concepts of „impulsive" and „continuous" force has never before been carried out (with one exception[11]), on reasons similar to those which lead Guicciardini and Cohen to their insufficient presentations of the second law. The reasons are that scholars often rely on the opinions of authorities and make use of unwarranted presuppositions in matters which seem too difficult for an independent investigation. If confronted with inconsistencies, they often resort to again unwarranted authoritarian statements. Thus an erroneous presentation of a principle as basic as Newton's second law of motion may continue through generations.

If one wants to investigate this matter profoundly, one will have to base the research on Newton's method of first and ultimate ratios which, in eleven Lemmata, is introduced in the Principia, book I section 1, as Newton's mathematical tool; and of course this method deals with measurement, i.e. — to spite Cohen — with the problem of dimensionality of physical magnitudes.

Lemma X concerns the concept of „force". The germ of it reads (according to the Cohen-Whitman translation): „The spaces which a body describes when urged by any finite force ..... are at the very beginning of the motion in the squared ratio of the times."[12]

This measure — or dimension — „space over square of time" [L/T²], connected to continually accelerated motion as the dimension of acceleration a, has already been mentioned above as Galileo's finding. Newton, however, doesn't speak of a constant continuous acceleration „space in squared ratio of the times" of a continuously accelerated motion, rather he confines the validity of the measure [L/T²] to „the very beginning of the motion". This is due to the fact that in Lemma X he doesn't refer to a continuous, rather to a finite force, to quote Newton's Latin: „Spatia quae corpus urgente quacunque vi finita describit....sunt, ipso motus initio, in duplicata ratione temporum"[13]. „Spatia quae corpus urgente quacunque vi finita describit" — that is: „The spaces a body describes if urged by a finite force".

The matter has to be a bit expanded since it concerns a main difference between Newton's authentic theory and classical mechanics. The latter knows only one „force", and this „force" is always and exclusively connected to continuous acceleration, and thus it is always a continuous force. This continuously accelerating force may also be called an „infinite" force, in so far as it produces an infinite increase of the velocity v, measured through the ratio of velocity per time unit [L/T²], or of the quantity of motion (mv), accordingly measured by [mL/T²], i.e. the „acceleration" a of a body m. The latter is the case with free fall, and with circular motion also, where the direction of motion is changed ad infinitum.

But Newton's theory knows different concepts of „forces" with different effects on a body's state of rest or motion: A concept of a finite „impulsive force", producing finite quantities of velocity or motion, or of changes of motion, is introduced in his work (in def. 4 and in the second law) under the name of „vis motrix impressa", the impressed motive force. It is this finite impulsive „vis motrix impressa" to which Newton refers in Lemma X as „quacunque vis finita" (i.e. any finite force). A different concept of infinite „continuous" force, as but a source (see def. 4) of continually emerging impressed forces to generate continual changes in the motion of bodies, is present in his work as „vis centripeta", the centripetal force.

The case will be more clarified by the following two diagrams. Let a body, urged by an infinitely or constantly accelerating force, start its motion in A. The measure [L/T²] of this acceleration will then be represented by the straight line AB to show that this measure in this case is not confined to „the very beginning of the motion only" (as Newton's term „ipso motus initio" should be rendered precisely), but is valid at every stage of progress of this motion, from its beginning to infinity (figure 1). Now, on the contrary, let the body start in A, urged by a finite impulsive force which produces a finite velocity of motion. In this case, the acceleration of the body will show a maximum at the very beginning of the motion, and will reduce to zero when the body reaches its un-accelerated, uniform straightlined motion, i.e. the momentum generated by the impulsive „impressed force" (figure 2). This development of acceleration which is represented by the straight line AB in fig. 1, will be given in fig. 2 by the curved line AC.

In fig. 1, the velocities v respectively the motions or momenta mv produced in times AC, AI, AO, are given by CB, IF, OP. In fig. 2, the velocities v respectively the motions or momenta mv produced in times AD, AE, are given by DB, EC.

It should be noted that fig. 1 is similar to Galileo's diagram representing the development of uniformly accelerated motion in his „Discorsi" of 1638[14], while fig. 2 is similar to the drawing Newton uses in the Principia to explain the action of a „finite" impulsive force according to Lemma X:

Fig. 3 is taken from the Discorsi, Third day, section „De motu naturaliter accelerato," illustration to Theorema II, Propositio II, Corollarium I. As Galileo deals with the free fall of bodies, in his diagram point A, where the motion starts from, is the top of the figure, and OP is the base of the upside down triangle AOP.

Thus we can better understand Lemma X after we have freed ourselves from the general, but mistaken belief according to which Newton's Principia should deal with always continuously accelerating „centripetal forces" only. Quite the contrary, Newton's def. 4 of „vis motrix impressa" makes it clear that the concept of a finite „impressed motive force" for Newton is basic, as it states that a (continuously acting) „vis centripeta" is always but a source of such impressed forces. Says Newton, in the Scholium to follow def. 8: „The causes which distinguish true motions from relative motions are the forces impressed upon bodies to generate motion. True motion is neither generated nor changed except by forces impressed upon the moving body itself." Motion is neither generated nor changed except by forces impressed. Vis impressa, the impressed finite force, is the basic concept of Newton's theory of motion. This can also be seen in Newton's first law of motion, where we read that „every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by forces impressed" (my emphasis).

Keeping this in mind, we are ready to understand the reason of Newton's demonstration of Lemma X. The reason is to show that every force, as a cause of motion, which basically is always a finite impulsive force F_i, at the very beginning of (the production of its proportional) motion DB, EC etc., but at the very beginning only, can be regarded as a continuously acting force F_c, and thus it can be computed according to Galileo's space-over-time-squared-law of uniformly accelerated motion.

And what was this demonstration of Newton's good for? It was good for the proof that the effect of an accelerating „vis centripeta" on the motion of a body, which infinite force generates equal finite „impressed forces" in equal times to produce equal velocities (of motion), or changes of velocities (or changes of motion) without end, can correctly be computed according to the space-over-time-squared-law, even though the measure or the dimension of the generated „impressed (finite) forces" will fulfill this Galileian law „at the very beginning of the produced motions" only. This can now be understood as the essence of figure 5 which Newton, immediately after the methodological introduction of sect. 1, presents as an illustration to sect. 2 „To find centripetal forces", Prop. 1 Theorem I[15].

The diagram shows how from an infinitely accelerating „centripetal force", directed to point S, there originate finite forces, which are impressed on the moving body at A, B, C, D, E, F, etc., in order to produce finite changes in the direction of motion which (by composition according to the laws of motion, Corollary I) deflect it from ABc, BCd, CDe, DEf, etc., to a path ABCDEF that in the limit describes a circular motion around the centre S.

III

One question remains for the careful reader: If impressed impulsive forces F_i to produce finite motions (or finite changes of motions, or momenta) can only at the very beginning of the motion (i.e. immediately when e.g. starting from rest) be measured according to the space-over-time-squared-law, how can such forces then be measured in general, say without this confinement to the very beginning of the motion? Newton clearly answers this question with his already quoted Second Law, to state that such forces are proportional to the produced motions or momenta, respectively to the produced finite changes in motion (including changes in the direction of motion). In Section 1 above we have found that the formula F_i = Δ(mv) × C should correctly represent Newton's second law. So, if we want to unveil the geometric measure, i.e. the dimensions of Newton's F_i, we shall have to consider the dimensions of the product Δ(mv) × C. As the dimensions of the change of momentum Δ(mv) according to Newton's definition of „motion" (def. 2) are known to be [mL/T], our task will be to find the dimensions of C.

Now, if we should ask our guides Cohen and Guicciardini for help, we would feel somewhat disappointed. Cohen, as we have stated above, cannot see any problem here since he treats finite forces F_i (for which Cohen writes F ∝ d(mV)) as if they were generally identical with (i.e. the same kind of force as) infinite forces F_c (for which Cohen writes F ∝ d(mV/dt)). Moreover, Cohen ignores any factors of proportionality here, alleging that Newton, having conceived „a dimensionless physics", had not to bother with such things. Consequently Cohen falls back to the inacceptable position of simply identifying Newton's finite „impressed motive force" of the second law with Newton's „vis centripeta", and moreover with the infinite accelerating concept of „force equal (not proportional!) to mass times acceleration" of classical physics as well[16].

Surprisingly, Cohen somewhat later pretends to have understood the theory of proportions as Newton's most elementary mathematical tool. Especially as far as the application of proportion theory to relations of magnitudes of a different kind is concerned, Cohen, stating that Newton „boldly" allows „that a quantity is proportional to a quantity of a wholly different kind"[17], is well aware of Newton's use of „mixed proportions", i.e. of the applicability of proportion theory to relations of heterogeneous magnitudes. And this is very clear and true the contents of Newton's Scholium following (not by chance) immediately to Lemma X, the Scholium giving some rules for the handling of relations between „quantitates indeterminatae diversorum generum", i.e. variable magnitudes „of different kinds" (transl. Cohen-Whitman), as Newton does it in the preceding Lemma X (i.e. relations of such magnitudes as „force", „time", and „space"). However Cohen, in his „Guide", dedicates only five insignificant lines to that Lemma, and none at all to the said most important Scholium[18].

Turning now to our second guide Niccolò Guicciardini, we too shall find no answer to our question, since he, presupposing the „classical" F = ma-concept as Newton's only concept of „force" in general, has no eyes for an impulsive finite „vis impressa" to produce finite proportional changes of motion. Actually, in his interpretation of Lemma X, Guicciardini mistakes Newton's finite force, ignoring the term „finite", for a variably accelerating force. Moreover, he raises our confusion to a higher level, as he steers clear of our question by simply alleging — in flagrant contradiction even to Cohen — that Newton was not at all able to form a proportion between a „force" and a „change of motion", because his proportion theory „does not allow the formation of a ratio between two heterogeneous magnitudes"[19].

Alas, again. If Newton was not able to form a ratio between force and change of motion, how at all should he have been able to form even an equation (!) F = ma between these heterogeneous unequal magnitudes of a different kind then? Should not the correctly understood heterogeneity of force (cause) and change of motion (effect) yield a striking argument against the idea to ascribe the equation F = ma to Newton? Or, in other words: Is not the equation F = ma an evident mathematical illustration of Leibniz's principle „causa aequat effectum", applied to a continuously mass-accelerating cause F? And, as far as Newton's use of proportion theory is concerned: Everybody who reads the Principia, the Scholium following Lemma X, will immediately see that Guicciardini's view contradicts not only Newton's clear words, but also Cohen's quite correct interpretation. Moreover, as students of the history of proportion theory from Euclid via Tartaglia to Galileo, Torricelli, and John Wallis, do know, Guicciardini's view ignores and contradicts historical facts which are established by documentary evidence. There is absolutely no doubt that Newton of course was in possession of the full Euclidean theory that included the theory of proportions of heterogeneous magnitudes (incommensurables). And it was exactly this knowledge which allowed him to state that a quantity is proportional to a quantity of a wholly different kind (to make use of Cohen's terms), as did already Galileo, when he formed the ratio „space over time squared" (a ratio of quantities of a very different kind) to measure uniformly accelerated motions of e.g. falling bodies.

IV

Let us now concentrate on the problem of the constant of proportionality C that is as evidently required by Newton's second law as it is absent in the „classical" mispresentation of this law. From Newton's Lemma X we know that a finite force F_i can in the limit be measured in the same way as an infinite force F_c. According to Lemma X, Corollary 3, the spaces [L] described by a body [m] under the influence of any force F_c, at the very beginning of the motion are as the product of the force F_c and the square of the time [i.e. T²]:

L ∝ F_c × T² (1)

The measure of F_c then will be F_c ∝ L/T² (2)

as it is stated in Newton's Corollary 4 to Lemma X. Now, instead of this measure [L/T²], I shall make use of the mathematically identical measure „velocity over time" [v/T]. Thus I obtain

F_c ∝ v : T (3)

which proportion is equivalent to the statement that the force F_c is to some hitherto unknown constant magnitude X, as the velocity v is to the time T:

F_c : X = v : T = constant (4)

We should always be aware that this quaternary proportion is valid at the very beginning of the motion only. Now, to unveil the identity of X, we can make use of another such limited proportion which e.g. Roger Cotes introduced, in his preface to the Principia's second edition (1713). According to Cotes, it results from simple mathematical reasoning that the force, at the very beginning of the motion, (not only is proportional to the constant relation v/T, but also) is proportional to the spaces described. Writes Cotes: „The rectilinear spaces described in a given time at the very beginning of the motion are proportional to the forces themselves"[22], that is to say

F_c : L = constant,

as well as (from (3)) v : T = constant

so that we obtain by composition

F_c : L = v : T (5)

Remember now that F_c = F_i at the very beginning of the motion. Consequently, L means an elementary finite length which is necessarily a constant element of space. However, since we are interested in the measure of the proportion of the force F_i to velocity v, or to motion mv, or to change of motion Δ(mv), as it is stated in Newton's second law, we may obtain by alternation[23]

F_i : Δ(mv) = L : T = constant [L/T] (6)

The measure, or the dimension, of the factor of proportionality to connect Newton's „vis motrix impressa" with its effect „mutatio motus" on the state of rest or motion of a body, now is unveiled to be given by [L/T], that is: constant element of space [L] over constant element of time [T].

The true measure, or the dimension of Newton's finite „impressed force" F_i then will arise from

F_i [mL/T × L/T] = Δ(mv) [mL/T] × C [L/T] (7)

One should be well aware that this measure of F_i cannot be represented as a product mL²/T² of mL/T × L/T, because the first L/T stands for a variable velocity, whilst the second L/T stands for a constant relation of elements of „space" or length [L] and time [T]. It is clear that a product of a variable [L/T] and a constant [L/T] cannot be represented as the square [L²/T²] of the variable or the constant. Consequently, one would be misled if one would think of the above developed measure of „force" as a representation of the concept which Newton's philosophical antipode G.W. Leibniz left to physics under the name of „vis viva", the living force, today known as (kinetic) energy, with measure or dimensions [mL²/T²].

Nevertheless, it is interesting to see here how closely the Leibnizian concept of „living force" [mL²/T²] is related to Newton's „vis motrix impressa". As a matter of fact, Leibniz's concept results from ignoring the limitation of Newton's considerations „to the very beginning of the motion only", i.e. from taking the dimensions [L] and [T] of C not as constant elements of space and time, but rather as variable measures of any variable lengths and times, thus destroying the proportion of Newton's second law in favour of an equality of cause and effect[24], and generalizing eq. (5) at will, as a measure of any acting force at any variable time, and at any state of motion.

In fact, if one does not think of a finite force F_i, as Newton did, the dimensions of which force only at the very beginning of the motion are given by the measure [mL/T²], but of an infinite constant force F_c, the dimensions of which are always given by [mL/T²], it can clearly be seen how the Leibnizian concept of kinetic energy [mL²/T²] results from eq. (5) solved for F_i, (which process is analogous to computing „kinetic energy" as space integral of infinite force according to the Leibnizian calculus). Note that in this case there appears no constant of proportionality, because its dimensions [L/T], erroneously treated as variables, are confounded with the dimensions of the variable „velocity" to form the squared space-over-time measure of this specific Leibnizian quantity of „living force". And this may well have been one of the reasons why Newton accused those „who confuse true quantities with their relations and common measures" to „corrupt mathematics and philosophy"[25], and why he called Leibniz's calculus „the analysis of the bunglers in mathematics"[26].

In Newton's authentic theory of motion, as we have seen above, the „generalized" measure of the basic finite concept of force F_i is not a „squared", rather a „linear" one, to be represented by

F_i = (mv) × C, or the equivalent F_i = p × C (8)

with p = mv = momentum. Eq. (8) shows a close relationship between Newton's „vis motrix impressa" and the equally „linear" concept E = p × c, or E ∝ p of the modern theory of propagation of light (in special relativity and quantum mechanics), with the constant of proportionality c to represent the absolute constant „vacuum velocity of light" [L/T].

V

Another investigation for the true and complete dimensions of „force" in Newton's authentic theory can be performed if one follows Newton's line of reasoning in the Principia, Book I, Section 8, proposition 41 concerning the determination of „the orbits in which bodies revolve when acted upon by any centripetal forces". Extended analyses of this geometric proposition of Newton's are given by I.B. Cohen[27] and by N. Guicciardini[28]. Unfortunately, their common method „in order to facilitate the understanding of this geometrical formula" that Newton presents in prop. 41, is to „betray (!) Newton and translate it into more familiar Leibnizian symbolic [not geometric but algebraic] terms", as Guicciardini puts it[29]; Cohen accordingly alleges that „Newton's seemingly (!) geometric language enables us to translate his presentation rather directly into the more familiar [algebraic] algorithm of the Leibnizian calculus"[30], and so does Guicciardini, as he states that Newton's geometry „can be easily translated into (Leibnizian) calculus terms by substituting infinitesimal linelets for Newtonian moments (or Leibnizian differentials)"[31]. In the following we shall see how this very substitution ignores the decisive difference between Newton's geometrical method and the Leibnizian calculus, and thus corrupts Newton's fluxional method as well as his theory of motion by rendering an increment of a velocity (which is conceived as a elementary, finite, constant quantity in Newton's method, as will be shown) into a Leibnizian variable differential ds/dt.

Newton's prop. 41 draws on the preceding prop. 39. Both propositions are illustrated in the Principia by the following diagrams.

I shall concentrate on prop. 39 which concerns the case of „a body ascending straight up or descending straight down" from A, following the straight line ADEC, under the influence of a centripetal force of any (variable) kind. The task is put to find „the velocity in any of its positions and the time in which the body will reach any place; and conversely". — As the body falls from A in the straight line ADEC, „let there be always erected from the body's place E the perpendicular EG, proportional to the centripetal force in that place tending toward the centre C; and let BFG be the curved line which the point G continually traces out." Now — says Newton — „at the very beginning of the motion let EG coincide with the perpendicular AB; then the velocity of the body in any place E will be as the straight line whose square is equal to the curvilinear area ABGE. Q.E.I".[32]

In the subsequent paragraph to prove the proposition, Newton writes:

„In the straight line AE take a minimally small line DE of a given length, and let DLF be the location of the line EMG when the body was at D; then, if the centripetal force is such that the straight line whose square is equal to the area ABGE is as the velocity of the descending body, the area itself will be as the square of the velocity, that is, if V and V + I are written for the velocities at D and E, the area ABFD will be as V², and the area ABGE as V² + 2VI + I², and by separation [or dividendo] the area DFGE will be as 2VI + I², and thus DFGE/DE will be as (2VI + I²)/DE, that is, if the first ratios of nascent quantities are taken, the length DF will be as the quantity 2VI/DE, and thus also as half of that quantity, or I × V/DE. But the time in which the body in falling describes the line-element DE is as that line-element directly and the velocity V inversely, and the force is as the increment I of the velocity directly and the time inversely, and thus — if the first ratios of nascent quantities are taken — as I × V/DE, that is, as the length DF. Therefore a force proportional to DF or EG makes the body descend with the velocity that is as the straight line whose square is equal to the area ABGE. Q.E.D."

I shall now concentrate on the first „Q.E.D.", i.e. the proof for the task to find the velocity of the body in any place E. My aim is to make explicit the geometric dimensions of the quantities involved in units of „space" [L] and „time" [T], in order to unveil the geometric dimensions of the centripetal force involved.

Note that the centripetal force is always given through the lines AB, DF, EG etc. perpendicular to AC. Now, if (according to Newton) „the first ratios of nascent quantities are taken, the length DF [which represents a centripetal force F_c] will be I × V/DE." Since I and V mean velocities and DE means a length, the dimension of the variable centripetal force F_c represented by DF is given through I[L/T] × V[L/T] × 1/DE[1/L]. Taking into account that the velocity I according to Newton means an „increment" of velocity, that is the velocity which is given through the rate of the „minimally small line DE of a given length" over the again minimally small „time in which the body in falling describes the line-element DE", and taking into account also that the minimally small „given length" DE conceptually means an elementary constant quantity of length [L], the „increment I of the velocity" will represent a constant quotient of an elementary unit of space over an elementary unit of time; I [L/T] = constant. From whence it follows that in Newton's above analyzed formula F_c = I × V/DE the only variable quantities are given through F_c and V. Consequently, we find that the relation of these variables, F_c/V = I/DE [L/T] × [1/L], must result in a constant with dimension [1/T]. And this result literally says that the quantities of centripetal force F_c and generated velocity V are proportional, connected by a constant factor of proportionality with dimension [1/T]. So we may interpret this result in harmony with Newton's def. 7 of the quantity (i.e. the geometric measure) of an accelerative centripetal force, according to which the centripetal force F_c is proportional to the produced velocity V in a given (i.e. elementary constant) time T; the „given time" 1/T then means the dimension of the „constant of proportionality" between this centripetal force and the proportional increment of velocity. Consequently we obtain for Newton's def. 7 and 8, with symbols F_c for „accelerating centripetal force", v for „generated velocity", and m for „mass", and with constants of proportionality and their dimensions made explicit:

• (def. 7) F_c/v = constant [1/T]
• (def. 8) mF_c = weight G; G/mv = constant [1/T].

One should note, however, that v in both cases means an increment of velocity, i.e. that „first" velocity which results from the quotient of a first given minimal length over a first given minimal time as a constant quantity.

Now, if we want to shift from F_c to F_i, in order to obtain the generalized measure of the impressed force F_i, since Newton allows F_c as a measure of an impressed force F_i at the very beginning of a motion only, we must take into consideration that e.g. from some weight G [mL/T²] as a source, an impressed force as a measurable quantity will spring off (according to Newton's def. 4) if, and only if the weight (the body) will actually have moved at least through a minimally small distance or length [L]. Consequently, the already (in the past!) „impressed" force F_i which is proportional to the already performed (!) motion mv according to Newton's second law, will be measured by the product of (weight G or) centripetal force F_c times L. And this measure F_i = F_c × L = mv × [1/T] × [L] = mv × [L/T] unveils that the proportion F_i : mv (as stated in Newton's second law) results in a constant factor with dimensions [L/T], which I have baptized the „Newtonian Constant". Q.E.D.

This analysis shows and demonstrates how powerful dimensional analysis can be applied to Newton's ratios and proportions, if one only proceeds carefully according to Newton's clear words, and if one rejects Guicciardini's proposal to betray (sic!) Newton by inconsiderately rendering his concepts into those of the Leibnizian calculus. As we can see now, the main difference between Newton's and Leibniz's concepts concerns the underlying structure of time and space. Since Newton holds a realist „quantized" view which implies real elementary equal (and thus constant) particles of „space" (length, [L]) and time, [T], his theory, when dealing with spaces and times at the very beginning of motion, or with an increment of velocity as well, must necessarily accept these elementary quantities as natural constants to constitute true geometric proportions between variable finite quantities such as „impressed force" and „generated motion" as soon as these quantities have appeared in reality. The variable quantities of spaces really traversed and times really elapsed, measured in relation to the absolute scales of space and time as represented by their constant elements [L] and [T], will then measure the variable velocity v of a really performed motion mv.

Leibniz, on the contrary, who conceived space and time not as real „absolute" entities, but only as structureless mathematical continua, consequently treats every appearing quantity of space (length) and time, and every increment of velocity always as a variable, even in the limit (Newton's „ipso motus initio"), as it can be seen for instance in the case of the differentials ds/dt and dv/dt. Since he doesn't accept any constant natural elements of space and time, he inevitably must destroy natural proportions based on such constants, in particular the proportion between force (cause) and motion (effect). In the case of how to measure a certain finite impressed force which has produced a certain finite motion, he must from G × L = [mv/T] × [L], by taking L and T for variables l and t, proceed to a measure mv × l/t = mv² [mL²/T²] — the well-known „squared" measure of „living force" (the later „kinetic energy"). This is the „squared" concept which he, in the vis-viva controversy, from 1686 on promoted.

VI

The finding of a „Newtonian Constant" C [L/T] as a necessary part of Newton's second law of motion after all has settled the question which from 1686 on had nourished the vis viva controversy concerning the question of how to measure a finite impressed force. This result means certainly a decisive step in the full evolution of the geometric theory of motion of Galileo and Newton. It has been known for long that „classical mechanics", as it is taught in contemporary textbooks, differs very much from the teaching of these fathers of modern science. As we now can see, the main difference concerns the concept of impressed force. It concerns a constant of proportionality with dimensions „space over time" which had got lost in the 18th century when the synthetic-geometric theory of Galileo and Newton declined, as their followers rendered the language of rational mechanics into the algebraic-arithmetic terms of Descartes and Leibniz. „(Even) In the hands of the early Newtonians, Newton's text moved from being a work in philosophy toward being the foundation of modern science" (Margaret C. Jacob).

Our careful research now shows that the theory of analytical mechanics in the shape it has attained since the end of that century resulted from a violent and erroneous process of reducing geometric proportions to algebraic equations, erroneous and violent in so far as constants of proportionality were banned, transformed into variables, and cancelled at will.

Why do I call this process „erroneous", even though it brought forth so powerful a tool for mechanics and engineering as analytical mechanics certainly is? The answer is: because this process, through the above shown corruption of Newton's theory, created a law of motion „F = ma" which, as is well-known, proved deficient 100 years ago, and had to be replaced in modern physics by a better concept based on that very constant of proportionality which now has been revealed as an erroneously omitted, and for 300 centuries lost part of Newton's true theory. I mean, of course, that absolute constant with dimensions „space over time" which, under the name of „vacuum velocity of light" c [L/T], governs the most of modern physics. It should be noticed here that „the view that a formal identity between mathematical relations betrays the identity of the physical entities involved harmonizes with the spirit of modern physics. Physical entities which satisfy identical formalisms have to be regarded as identical themselves" (Max Jammer)[36]. Consequently, the Newtonian constant c [L/T] as a part of Newton's true theory will guarantee this theory the same exactness as we know it from the theories of modern physics thanks to the efficiency of the constant called „vacuum velocity of light" c [L/T] as a necessary part of a realist theory of motion.

Let me finally demonstrate that this constant „space over time" is already present in Galileo's teaching. Never has it been considered before which set of units Galileo used in his theory of motion. How — that is: by means of which scale, and in which units — did he measure lengths, how distances of fall? How — that means: relative to which scale, and in which units — did he measure times? Sometimes problems can be solved by asking the right questions. The answer to our question is that Galileo (as well as Newton afterwards) made use of a set of units of „space" [L] and „time" [T]. At the beginning of the most important part of his „Discorsi" of 1638, when he introduces the new theory of motion, Galileo draws two simple straight lines, one of them representing a scale of „space" (length, distance) to measure variable „spaces" (lengths, distances) in units of space, the other representing a scale of „time" to measure variable times in units of time.

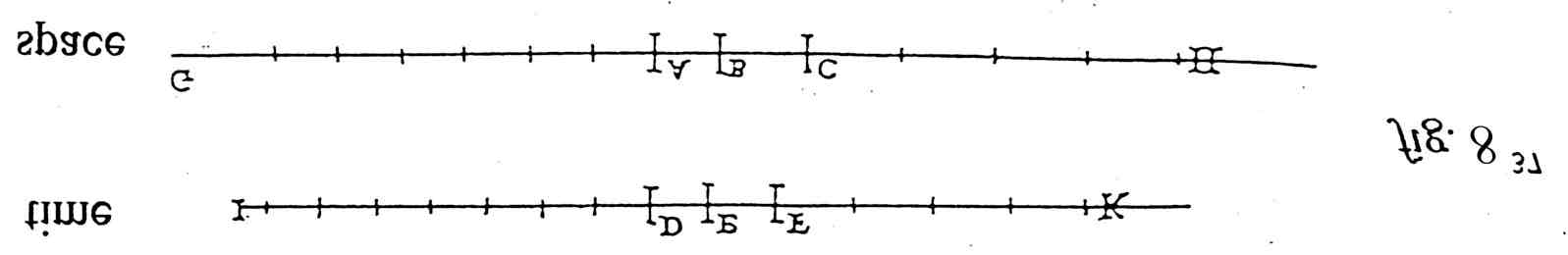
It is easy to understand that he who wants to measure the „spaces" and the „times" of bodies in motion will need two scales for this purpose. Galileo's scales contain, and are composed of, constant elementary parts or units of space [L] and of time [T], following one another ad infinitum. Thus Galileo's two innocent straight lines symbolize geometrically the metrics, i.e. the quantization of absolute space and time, and the infinity of space as well as that of time much in the way Giordano Bruno had taught it literally. This infinite scales of space and time, of course, in order to serve really as scales relative to which relative spaces (lengths, distances) and relative times can be measured, must necessarily be graduated, that is composed of finite constant elementary parts of „space" [L] and „time" [T]. And these elementary parts evidently stand to each other in a constant relation, which means that the elements of space and time are proportional to each other[38]. The constant proportion [L/T], then, can be called the parameter which represents the metrics of the space-time frame of reference of motion, as it lies behind the authentic theory of motion of Galileo as well as of Newton[39]. There is no doubt that this theory ever since required and tacitly included such a frame of reference of Euclidean shape, because a theory of motion without any such frame wouldn't make any sense. There is also no doubt that this frame is present in Galileo's drawing to explain the propagation of uniformly accelerated motion as in part already shown above, Section II fig. 3. The figure clearly reveals the always constant elements of space, BE, EC, FN, NG, GH, HI, PR, RQ, etc., and the always constant elements of time, AC, CI, IO etc. which together form the space-time frame of reference AOP wherein the accelerated motion starting in A takes place.

If we now carefully analyze the proportions Galileo explains, we shall see that e.g. the rate of the increments of space traversed and the corresponding increments of time elapsed, always results in a constant [L/T] — the constant which, since I in 1983 found it in Newton's second law, I have termed „Newtonian Constant". Guicciardini and others, who thought that Galileo only had formed series of homogeneous magnitudes such as l₁:l₂:l₃:l₄, and had compared this series with others, e.g. a series of times t₁:t₂:t₃:t₄, etc.[40], should see that according to Euclid's definition book 5 def. 6, magnitudes l and t which have to each other the same relation (that means e.g.: l₁ has to l₂, l₂ has to l₃, l₃ has to l₄ etc. the same relation as t₁ has it to t₂, t₂ to t₃, t₃ to t₄ etc.), are termed proportional, i.e. that they result in a constant relation L/T. Since in Euclid's Greek „relation" is „logos", it is interesting to see that „proportional" in Greek is „analogos" which clearly indicates the difference between a ratio (logos) of homogeneous magnitudes, and a proportion (analogos) of heterogeneous magnitudes. The term „proportion" should then above all indicate a constant relation between heterogeneous magnitudes.

As we can see now, the term „proportional" in Galileo's and in Newton's theory, especially the „proportionalem esse" in Newton's second law, provides the constant space-time frame of reference and measurement of „spaces traversed" and „times elapsed" as variable values for the measurement of variable velocities and motions. No wonder, then, that the proportionality of these magnitudes to their generating forces, if made explicit in an equation, unveils the parameter L/T of an Euclidean space-time frame of reference.

VII

After all, the constant C [L/T] being a necessary part of Newton's second law, represents nothing else but the metrics of the Euclidean frame of reference of motion which so many scholars in the past have thought to be not explicitly exposed (though implicitly presupposed) in Galileo's and Newton's theory. As this constant now stands clearly before our eyes, it stands there as a parameter of the metrics of absolute space and absolute time to serve as constant absolute scales for the measuring of variable and „relative" spaces and times, „relative" in so far as they are measured, and only can be measured, relative to these invariant scales of absolute space and of absolute time — a view which should agree with the contents of Newton's extensive Scholium on space, time and motion to be read in the Principia, after def. 8. If accepted as a necessary part of the second law of motion, this constant, by showing Newton's concepts of absolute space and absolute time as indispensable mathematical constituents of the theory of real true (i.e. absolute) motion, will heal „classical" mechanics from its main defect „instantaneousness" (i.e. the unreasonable concept of motion to generate not in space and time, but instantaneously, i.e. without any elapse of time), thus giving back to Galileo and Newton the undefiled fame they deserve.

Alfred North Whitehead once said that Newton's Scholium on space, time and motion, and Plato's Timaios, contain the only two relevant cosmologies of western thought. But he didn't realize that Newton's philosophy of nature was heavily corrupted when, in the course of the 18th century, adherents of the relativist theory of motion of Descartes and Leibniz, by denying the existence of absolute space and absolute time (i.e. by denying the existence of natural scales for the measurement of variable times and spaces), and by equating the cause „force" with its effect on motion, omitted the constant of proportionality, thus removed from the theory of motion together with the concepts of absolute space and absolute time the underlying absolute space-time frame of reference, and established a „classical mechanics" which, under the false colours of Newtonianism, in fact rests on Leibniz's relativism as to space and time, and on his concepts of „vis mortua" (F = ma) and its space integral „vis viva" (E = mv²)[41].

Nothing in science can really be understood without the help of philosophy. In order to understand and reestablish the true authentic theory of Newton (and of Galileo), one must consider the philosophy of space and time on which it is founded, and follow an advice of well — I. Bernard Cohen, who wrote some years ago: „We must be careful lest we bind Newton's thinking in an intellectual strait-jacket that satisfies our own requirements at the expense of understanding his."[42]

One could not have said it better.

Postscript

Only after I had finished this paper I read Herman Erlichson's article on „Motive force and centripetal force in Newton's mechanics", Am. J. Phys. 59 (1991), 842-9. There are some agreements, but also some disagreements to be noted as follows:

1. I agree with Erlichson's statement that Newton's basical concept of „motive force" „originated in the consideration of collisional forces" (p. 843), and that generally „Newton was thinking of the finite change of motion (proportional to the finite motive force)" (p. 843, my italics).
2. I disagree with Erlichson's view that „motive force" should always act instantaneously (which is physically impossible, as we know from modern physics). Above I have tried to develop the mathematical description of impressed motive force and change of motion generated in space and time, as I find it in the Principia, especially in Lemma X.
3. I disagree with Erlichson as he identifies Newton's general concept of a (finite) „motive force" with Principia, def. 8. In my view, def. 8 means explicitly that „the motive quantity of centripetal force is the measure of this force that is proportional to the motion which it generates in a given time". (my italics). Erlichson, however, by inadmissibly generalizing this measure of centripetal force to mean plainly „force" or „motive force", confuses it with Newton's general and basic concept of a finite „vis motrix impressa", the „impressed motive force" which is defined in Newton's def. 4, and appears again as part of Newton's first and second law.
4. I agree with Erlichson's result that Newton's „continuous treatment which defines force at a point is based on the limit of the polygonal treatment. Newton's concept of force is always based on motive force" (p. 849). I want to add, however, that one should not speak of „motive force" here, and not refer to def. 8, but of „impressed motive force" which refers to the traditional Latin technical term „vis motrix impressa" (well-known to Galileo for instance) that is clearly defined and developed in Newton's Principia not in def. 8, but in def. 4, and in the second law. I have indicated above the far-reaching consequences which follow from this finding, supposed one is ready to depart from the un-Newtonian idea of instantaneousness and, taking into account the real development of motion in space and time, reveals carefully the dimensions of this concept of „impressed motive force".