5. Inertia, the Innate Force of Matter: a Legacy from Newton to Modern Physics

Abstract

This paper refers to the hitherto unrecognised mathematical, physical and philosophical differences between Newton's "materiae vis insita" or "vis inertiae", and the concept of "inertia" as a quality of matter known in classical mechanics. Newton knows about a real immaterial "force" which accompanies matter like the soul accompanies living bodies. Consequently, I better had given the paper the title "Inertia, the Force Innate in Matter" in order to clearly express Newton's concept. However, the careful reader will certainly understand the paper's intention to show that an abyss separates Newton's "forces" from their materialistic identification with (qualities of) matter, and to show the power of authentic uncorrupted Newtonianism as an explanatory tool to be used in the interpretation of modern physics.

The paper for the first time consistently derives the true measure of Newton's concept of 'motive force', (mv × c), and the dimensions 'element of space L over element of time T' of the newly discovered 'Newtonian Constant' c [L/T], from Newton's Principia (Method of first and last ratios). Even though its English certainly is in need of improvement, it still provides a reliable source for the reader who wants to understand how the author came to reconstruct this concept, and why he believes that in the future it will be accepted as a foundation of the theory of motion and of true natural philosophy much better than everything that exists under this name today.

I. Introduction

For many scholars, the publishing of Isaac Newton's Principia in 1687 marks the beginning of a period of physics which they call the classical one[1]. Yet it is questionable whether Newton's "Mathematical Principles of Natural Philosophy"[2] actually represent what is known as physics today. The Principia is a foundation for a mathematical philosophy of nature as viewed by Plato. If physics is within the scope of this philosophy, then it also includes metaphysics as a presupposed knowledge of the absolute, of space and time, of matter, force and motion, of cause and effect; read the Scholium that follows the eight definitions introduced at the beginning of the Principia[3]. That is why physicists of the positivistic school of thought have had their problems with Newton since the time of George Berkeley and Ernst Mach[4], and why, as a result, many people are more familiar with the title than with the contents of the Principia.

In my view, this "bible of classical mechanics" (Max Jammer[5]) first and foremost represents the metaphysical elements (in the language of synthetic geometry) of exact science, "Metaphysische Anfangsgründe der Naturwissenschaft", as Immanuel Kant would have said. For, the "Erklärungen" (definitions) and the "Leitsätze" (propositions) which Kant formulates in his own work of this name in 1786[6] coincide with Newton's definitions and axioms both in their intent as a basic foundation, and partially also in their content; one only needs to compare the third proposition of Kant's main chapter 3 with Newton's First Law of Motion, the law of inertia.

In the present discussion, it will be established that the concept of inertia, among others, clearly shows that Newton's teaching not only goes beyond what we know today as classical physics, but also that it considerably differs from that subject. Afterwards, I will show that the Newtonian concept of inertial force could plausibly be used in solving certain open questions in modern physics such as the problem of the wave-particle dualism[7].

II. The Principle of Inertia in Classical Mechanics and Newton's "materiae vis insita"

1.

The classical principle of inertia says that a body always continues in its existing state of rest or uniform straight-line motion as long as no external forces act upon it. This should result from a basic characteristic of matter which we call inertia. Yet Newton's philosophy rejects explanations of nature by such hidden qualities of matter[8]. It recognizes the ability of matter to continue in its existing state as an effect of its own implanted force which Newton calls materiae vis insita, or vis inertiae, or even impetus[9]. Because the word vis simultaneously conveys the concept of both force and cause, Newton views the force of inertia as the cause of uniform straight-line motion[10]. Classical mechanics lacks this approach; due to an arbitrary generalization of Newton's concept of centripetal force (Principia, def. 5-8), it always equates force with acceleration, and considers the uniform straight-line motion to be without force, resulting in a "causal paradox" (C.F. von Weizsäcker[11]). Of course, such a limitation of the notion of force (which came about during the Enlightenment[12]) occurred without empirical foundation. It was rather the materialistic scientific ideology which, favouring the hidden quality of "inertia" of matter, eliminated Newton's spiritual materiae vis insita, and generally wherever it seemed to be possible, all immaterial forces of nature (which were, however, the essence of the Neoplatonic Newtonian Philosophy, as preached from the pulpit by Samuel Clarke as late as 1704[13]). Immanuel Kant, in his commentary to the above-mentioned proposition, also turned against the idea that inertia is more than the mere lifelessness of matter. He remarks that everything else would be hylozoism. But Kant overlooked the possibility that force as a quantity, instead of being a necessarily active principle, might also be a passive principle, or even the power of continuing in a steady state. Newton, for his part, describes the force of inertia exactly in this way in the Principia, def. 3. According to his Third Law of Motion, this force becomes active and acts externally only if and as long as an active external force is imposed on the body which interacts with the body's internal force[14].

The issue concerns the mechanism for the creation of a material change in the motion of a body through a non-material external cause, as well as the problem of psychophysical interaction (the matter-spirit relationship) which was a central theme of philosophy in the 17th century[15]. Newton solves this problem by assuming an interaction between external force (vis impressa) which changes motions, and internal force (materiae vis insita) which maintains motions, completely at the spiritual level. G. W. Leibniz, representing the antipode of that position, attempts to solve the same problem by proclaiming a priori an equality between causa and effectus[16], between force and change of motion, declaring this equality to be his "first axiom of mechanics"[17]. Conceived in this way, however, the identity of cause and effect implies that force becomes materialized, thus completely shifting the problem to the material level, where it already had been placed by the materialistic Cartesian theory of impact. Indeed, ever since that time, this materialistic concept became the foundation of classical mechanics, as it is shown by its paradigmatic principle that force equals mass times acceleration. Here, force is no longer a physical entity with an ontological status of its own, but only another expression for the rate of change of the material entity called motion.

2.

In the question of Newton's force of inertia, nothing would be gained by showing that Newton merely gives the name of force to what was called inertia in classical mechanics. Galileian-Newtonian experimental philosophy requires that physical entities be quantified mathematically. This doctrine accepts only quantities, i.e. the measurable, as real and as a subject of exact science. To illustrate the point, Newton once again points to the mathematical realizability of the force of gravity as a sufficient proof of its reality, a proof which does not loose its validity even if the phenomenon of gravity itself is not understood physically[18]. Similarly, the force of inertia, if it is to be physically real, must have its mathematical measure. Now this measure can be developed from the context of the Principia, with the Second Law of Motion pertaining to the external, motion-changing vis impressa serving as a starting point[19].

It is well known that scholars differ over the interpretation of this axiom in which Newton represents the external motion-changing force as proportional to the mutatio motus of the body. The controversy concerns the question as to whether mutatio motus is to be translated as change of motion, or whether Newton meant the rate of change of motion[20]. The wording of the Second Law as well as the contents of the commentary pertaining to it clearly favours the expression change of motion which could be translated into modern terminology by the expression Δ(mv), (where m is the mass, and v is the velocity of the moving body). This implies a finite change in the quantity of the measured motion (mv). If so, the associated proportional force also takes on a finite quantity, somewhat analogously to the conventional notion of impulse[21].

The controversy can be expanded to include yet another aspect: it concerns the proportionality (not equality!) of force and change of motion stressed by Newton. Many scholars now feel that the force F should be considered to be proportional to the mutatio motus interpreted as acceleration a, whereby the quantity of matter or the mass m of the body would be the constant of proportionality. Ernst Mach, for instance, thought that this formalistic approach could be used to define mass, because, as an opponent of the atomic theory, he mistrusted Newton's definition of mass[22]. Mach's interpretation, however, evidently fails because Newton utilizes neither the mere acceleration a nor the mere change of velocity Δv, but rather the change of motion (which is the quantity arising from the product of mass and velocity, our momentum) as the physical entity that is proportional to the force.

But if so, what then is the constant? Whether one symbolizes the mutatio motus by ma or by Δ(mv), the resulting proportion with a force F in any case presents the equations

both of which contain the hitherto unknown proportionality constant c.

This constant can under no circumstances simply be replaced by a "one" (without units) in order to remove it from the equation and perhaps obtain the formula F = ma[23]. For that would presuppose that the force F and its equivalent effect had identical measures, or, in other words, identical geometrical dimensions (units), which in itself would lead to the conclusion that they are one and the same[24]. In virtue of Leibniz's phrase causa aequat effectum his theory might appear to yield the identity between force as cause, and change of motion as effect; but Newton's teachings completely forbid such an assumption. Here, Plato's principle of the analogy (not identity!) of nature is valid[25].

But, as to the principle of causality, this analogy of cause and effect means that, although nothing is in the effect that was not already contained in the cause (as Newton knows[26]), one cannot reverse the sentence. Therefore, their mathematical relationship to each other cannot be identity, but only a proportionality[27]. Hence it follows that, the proportionality constant c being the quotient of these two entities of different measures, it too has a mathematical measure or dimension, or units of its own. Therefore it cannot be removed from the equation without destroying the proportion. All in all, if seen from the Newtonian point of view, the vis viva controversy which led to quarrels among the members of the learned world, starting with Leibniz's publication of 1686[28], and continuing up to the supposed solution of the problem by d'Alembert in 1743 (upon which, however, Newton himself never commented), poses the question about the measure of the constant c; knowledge of this constant yields knowledge of the measure of the force vis impressa. The measure of the vis impressa by the use of eq. (2) which is determined through the product of change of motion Δ(mv) and the constant c, leads one to see also that the equation of condition of the materiae vis insita. Indeed, if uniform straight-line motion (mv) results from an interaction between vis impressa and vis insita, and its further cause after the completion of the effect of vis impressa is only the vis insita that maintains the produced motion[29], then the measure of this matter-implanted force, which from now on will be represented by the letter E, should be given by

This mathematical-symbolic formulation reveals for the first time Newton's First Law of Motion in terms of a causal relation between motion (momentum) mv, and the moving body's vis insita E. Everything else depends on the measure, or the dimension, of the constant c.

3.

Newton's concept of vis impressa as a finite quantity which is proportional to a finite change of motion developing as an event in a finite time, solves the puzzle. This concept clearly results from Lemma X of the "Method of first and last ratios of quantities" where Newton explicitly investigates the effect of a vis finita[30]. The development of the idea of a finite effect (motion) from a finite cause (force) as an event which takes place in time was an illuminating insight indeed. Everyone will concede that, when a billiard-ball is struck, it does not instantaneously gain the velocity of motion that is proportional to the striking force, but rather this will take a finite time because, as Galileo has demonstrated, the ball must first conquer all the smaller velocities. Nevertheless, classical mechanics offers no adequate description for this phenomenon. Instead, in virtue of the Leibnizian identity between causa and effectus, the effect change of motion should - according to classical mechanics - emerge instantaneously[31] from its "cause", that is from the simultaneous and identical impulse of the same quantity. This identity of simultaneous, functionally interrelated entities, which is the substructure of analytical geometry within the framework of Cartesian coordinates, yields no causal-creative, but merely a deterministic picture of nature. Here might perhaps lie the deeper reason why Newton, but also Galileo and his disciple Evangelista Torricelli, preferred the synthetic geometry of the Ancients. As a matter of fact, Albert Einstein's critique of the concept of simultaneousness in contemporary physics which led him to introduce an additional time-axis in the context of Special Relativity, might in some way represent a recovery of the virtues of synthetic geometry.

Let us then, for a moment, accept Newton's proposals and oppose Leibniz, and let us take it for granted that a finite force E yields a continually (i.e. in the course of time) developing motion, (mv), which is proportional to it. In this case, the event of the creation of this motion will be characterized by a continual diminution of the increase of motion (or of the velocity of the creation of the motion) which starts from a maximum. The diagram below clarifies this description:

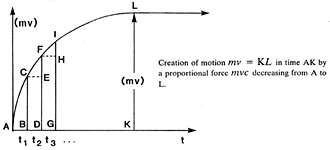
The distances, BC, DF, GI, represent the quantities of motion created during the times t₁, t₂, t₃, respectively; the distances BC > EF > HI represent the corresponding velocities of development (or the diminishing increase in the creation) of the motion. It is seen that, at the very beginning of the motion (mv) during the time interval t₁, the velocity of the generation of motion, or the increase of the quantity of motion, is equal to the velocity of the generated motion BC and has a maximum, inasmuch as it finally, when the motion in the time AK attains the quantity KL corresponding to the whole acting force, approaches zero. This first velocity, because it is a maximum, is apparently the same constant with different motions. This may be demonstrated by using Newton's "Method of first and last ratios of quantities" as follows: As the distances which bodies describe as an effect of some finite regular force are (according to Lemma X) proportional to the times squared at the very beginning of the motion, so that the first velocities are proportional to the first times (distance over time squared = velocity over time), these first velocities during equal first times must be equal for different motions; henceforth they shall be represented by the symbol c.

Now this constant initial distance-time relationship c of the developing motion must obviously be seen as a factor of proportionality between the force E and the created motion (mv). This can be confirmed through a proportion given by Roger Cotes[32], according to which the distances covered by a body at the very beginning of its motion[33] are proportional to the motive forces. In other words, these forces are to the distances as are (according to Newton's Lemma X) at the same time the first generated quantities of motion to the first times. This applies to the quaternary proportion E : l = (mv) : t (l is the initial distance, t is the initial time). From this statement, one can obtain a general relationship which no longer applies merely to the initial times (or to the very beginning of motion only), but which, by transposing the proportion, unrestrictedly yields E : (mv) = l : t, which l/t represents the proportionality factor of the relation of force E to created motion (mv) in accordance with Newton's Second Law of Motion. Indeed, in this case the creating forces are to the created motions as the initial distance l is to the initial time t; and with this constant ratio of the initial distance to the initial time, the emerging constant of proportionality is actually the initial developing velocity c established above, with dimensions or units [L/T]. Since this argument rests upon Newton's concept of absolute (i.e. real) space and time, it should come as no surprise that his theory tacitly contains this absolute space-time relation c as a natural constant linking mathematics to physical reality.

Remarkably, the ratio E : l = (mv) : t also provides the substructure of Leibniz's analytical theory of motion. If one solves for E, and if it is assumed that the initial space-time relationship is not a constant quotient of absolutes, but a variable velocity v as a quotient of only relative quantities, one obtains E = mv², which is the measure of Leibniz's living force vis viva[34]; and within this relative frame of reference, the constant c vanishes. This method generalizes the proportion which Newton strictly confines to the very beginning of motion, and thus it indicates a linear increase in motion, or constant acceleration, as the essence of an analysis which is in flagrant contradiction to Newton's approach[35].

III. Newton's Inertial Force and Modern Physics

Since the dimension of the constant c is known, eqn. (3) which defines the inertial force is completely resolved. One should be able to equate this Newtonian constant[36] with the constant c that dominates modern physics as the 'vacuum velocity of light'. In a consistent quantitative theory, the dimensions of a physical entity characterize its identity, and entities equal in dimensions are identical in character[37]. Here this identity of character is confirmed since both constants are absolute maximum velocities. By virtue of this identity, there appears an exciting connection between Newton's inertial force and the elementary conceptions of modern physics, for the mathematical combination of the quantity of motion or the momentum p through the constant c with another variable, E, which in this case is called energy, is, for instance, to be found in the Photon Theory of Quantum Physics. And the above-mentioned measure (mv)c of the inertial force E takes on the explicit form in the well-known non-relativist derivation of Einstein's mass-energy proportion[38].

Our E = (mv) × c also allows for a physical interpretation of the inertial force. Apparently it is an immaterial phenomenon that is associated with uniform straight-line motion proportional to that motion's measure (mv), namely the force of unresisted motion which in this case is not understood as the body's capacity for work or its kinetic energy, but rather as the real cause of motion, i.e. "the force of a body's motion" in the sense of Samuel Clarke, who demonstrated that the measure of this force must stand in a linear relationship to the velocity of motion, and that it can by no means be given through the Leibnizian mv²[39].

Whoever seeks experimental proof for this real physical phenomenon must remember that the force of inertia appears as an external action only when a body undergoes changes of motion (including changes of direction due to its vector character). Modern physics actually provides this experimental evidence through the diffraction phenomena which are produced by a beam of electrons that passes through a diaphragm, in the screen behind it (the beam being diffracted at the edges of the diaphragm), and which can only be related to immaterial wave phenomena. The dualism of waves and particles, a concept which has given rise to so much confusion and unsatisfactory speculation in both the physics and philosophy of the 20th century, turns out to be evidence supporting the Newtonian idea of the reality of immaterial, motion-accompanying phenomena or spirits, which are called matter waves or deBroglie waves in modern physics, and are mathematically described through the equation E = hν (h = Planck's constant, ν = frequency)[40]. Endowed throughout with this spiritual force "energy", the universe (which the adherents of pure reason had conceived to be lifeless[41]), lives again[42].

John Maynard Keynes, who in the 1930's studied unpublished papers from Newton's estate has said that Newton was certainly not the first harbinger of the mechanical age, but rather the last of the magicians[43]. Thus Newton could be perceived as a link in the chain that may have begun with Hermes Trismegistos who is considered to have brought man numbers, letters, science and art. It appears certain that Newton's legacy is not the deterministic, godless mechanics of, for instance, Pierre Simon Delaplace. Rather it is still waiting to be redeemed, and, as a daughter of time, it might perhaps construct the arch of western thought linking Plato to modern physics, and thus become the foundation for a realistic understanding of what occurs in quantum mechanics[44].

Notes